이원 로지스틱 개념 http://statnmath.tistory.com/86 및 모델 http://statnmath.tistory.com/87 은 링크 참조하세요.
이번 포스팅은 이원 로지스틱 회귀 예제를 들어 정리해보려고 합니다. 자세한 내용은 아래 링크 참조하세요.
http://statnmath.blogspot.ca/2015/08/case-study-binary-logistic-regression.html
Case Study: The Donner Party
Donner와 Reed 가족 87명이 웨건(마차같은거요~)을 타고 이동하는 도중 눈태풍에 갇히게 됩니다. 다음 해 봄, 40명만 구조되었는데요. 나이와 성별, 그리고 생사여부로 데이타가 이뤄집니다.
Reference: Gayson, D.K., 1990, "Donner Party deaths: A demographic assessment," Journal of Anthropological Research, 46, 223-42, and Ramsey, F.L. and Schafer, D.W., 2002, The Statistical Sleuth, 2nd Ed, Duxbury Press, p. 580.
[1] Data and Model
Response $Y_{i}$ : Binary variable; survived/died. (Binary Logistic이기때문에 y가 continuous 하지 않습니다!)
Predictors $X_{i}$ : 나이, 성별 of ith pioneer.
Odds in favor of success is $\frac{\pi}{1-\pi}$ & Log Odds: $\log \frac{\pi}{1-\pi}$
Model : $\log \frac{\pi}{1-\pi}= \beta_{0} + \beta_{1}AGE_{i1} + \beta_{2}SEX_{i2}$, i=1,...,45 Binary Logistic Regression
여기서 우리는 성별과 나이만 가지고 가족일원이 죽었는지, 혹은 살았는지 예측할 수 없습니다. 다만 살 확률 혹은 죽을 확률만 계산할 수 있는거죠.
[2] SAS Code - proc logistic
2.1. Default Code
먼저 SAS Code에 대해 정리해보겠습니다. proc logistic으로 해서 결과값을 구할 수 있는데요. 문제는 기본적으로 알파벳 순서로 되어있습니다. 즉, Y값이 survival, die로 되어있는데 알파벳 순서라면 die가 먼저 오겠죠. 그래서 die값이 default로 됩니다. 이렇게 프로그램을 돌리면 $\pi$=P(DIE)! 을 기준으로 결과값이 나옵니다.
그리고 성별은 categorical variable이기 때문에 class 명령어를 이용하여 여성과 남성이 각가 1과 -1로 구분하도록 합니다.
2.2. SAS Code - DESCENDING Options
그런데 $\pi$=P(Survival)! 로 하고싶으면 DESCENDING을 입력하면 됩니다.
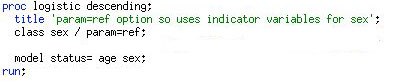
2.3. SAS Code - CLASS Options
마지막으로 성별을 1과 -1로 코딩하지 않고 indicator variable로 표현하고 싶으면 / param=ref; 명령어를 넣어줍니다. 그러면 $I_{Female}=1$ 여성일 경우, 0은 남성일 경우로 표현됩니다.
다음 포스팅에서 Wald Test와 Likelihood Ratio Test에 대해 정리해보도록 하겠습니다.
'공부정리 > Data Analysis 회귀분석' 카테고리의 다른 글
| Binomial Logistic Regresion (1) - Deviance, Global Likelihood Ratio Test (2) | 2015.08.22 |
|---|---|
| Binary logistic regression - 이원 로지스틱 회귀 (4) 예제 Wald Test, Likelihood Ratio Test (0) | 2015.08.17 |
| Binary logistic regression - 이원 로지스틱 회귀 (2) 모델, MLE (0) | 2015.08.14 |
| Binary logistic regression - 이원 로지스틱 회귀 (1) - Assumptions (0) | 2015.08.14 |
| [SAS] Two Way ANOVA 예제 (0) | 2015.08.13 |